Infos zur Simulation Doppelpendel

• Phi1 ist der Winkel von der Vertikalen zum ersten (roten) Pendel. Phi2 der Winkel von der Vertikalen zum zweiten (blauen) Pendel. (Diese Winkel sind im Bogenmass zwischen - Pi und +Pi).
• Grundlage zur Lösung der Bewegung des Doppelpendels ist die Lagrange-Gleichung: Die Energieformen sind die potentielle Energie Epot(Phi1,Phi2) und die kinetische Energie Ekin(Phi1,Phi2,Phi1',Phi2'). Die modifizierte innere Energie des Systems ist  L=Ekin-Epot.
  Die Bewegungsgleichungen lauten also:
  
  
  
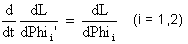
  Nach Auflösen dieser Gleichungen erhält man zwei Differentialgleichungen zweiter Ordnung in den Winkeln Phi1 und Phi2. Diese werden dann in vier Differentialgleichungen erster Ordnung umgewandelt, die dann mit dem Runge-Kutta-Verfahren gelöst werden können.
• Die Schrittweite h können Sie nicht grösser als 0.04 wählen. Die Lösung mit dem Runge-Kutta-Verfahren (ohne Schrittweitenanpassung) wird sonst viel zu ungenau.
• Klicken auf Step zeigt den nächsten Schritt (mit Schrittweite h).
• Klicken auf Run/Stop lässt das Programm laufen. Erneutes Klicken auf Run/Stop hält es wieder an.
• Vergessen Sie nicht, nach einer Änderung zuerst den Start-Knopf anzuklicken. Die Return-Taste genügt nicht!