Axiome von Kolmogorow (auch etwa Kolmogorov oder Kolmogoroff)

für Lebenslauf von Kolmogorw: Kolmogorow bei Wikipedia

Axiome der Wahrscheinlichkeitsrechnung

I. Jedem Ereignis E des Stichprobenraumes ist eine reelle Zahl P(E), seine Wahrscheinlichkeit, zugeordnet.

II. Für diese Funktion P: E → P(E), gilt:

• Die Wahrscheinlichkeiten sind nicht negativ:  P(E) ≥ 0.
• Die Wahrscheinlichkeit des sicheren Ereingnisses S ist eins:  P(S) = 1.
• Die Wahrscheinlichkeit, dass von zwei unvereinbaren Ereignissen entweder das eine oder das andere eintritt, ist gleich der Summe der beiden Wahrscheinlichkeiten: P(A B) = P(A) + P(B), falls A ∩ B = Ø

Diese Axiome wurden von A.N.Kolmogorow 1933 im Buch "Grundbegriffe der Wahrscheinlichkeitsrechnung" publiziert.

Mit Hilfe dieser Axiome (und den Gesetzen der Mengenlehre) lässt sich z.B. sehr einfach der sog. Additionssatz herleiten:

Additionssatz: Für zwei beliebige Ereignisse A und B gilt: P(A B) = P(A) + P(B) - P(A ∩ B)

Beweis:   A: Entgegengesetztes Ereignis von A ( A tritt genau dann ein, wenn A nicht eintritt)

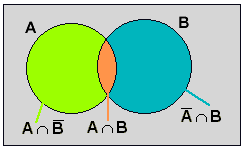
P(A) = P(A ∩ B) + P(A ∩ B)   →   P(A ∩ B) = P(A) - P(A ∩ B) P(B) = P(A ∩ B) + P(A ∩ B)   →   P(A ∩ B) = P(B) - P(A ∩ B) P(A B) = P(A ∩ B) + P(A ∩ B) + P(A ∩ B) P(A B) = P(A) - P(A ∩ B) + P(A ∩ B) + P(B) - P(A ∩ B), also P(A B) = P(A) + P(B) - P(A ∩ B)

Mathematics of the 19th Century A.N. Kolmogorov, A.P. Yushkevich