Gegeben: Kreislinie mit Radius r

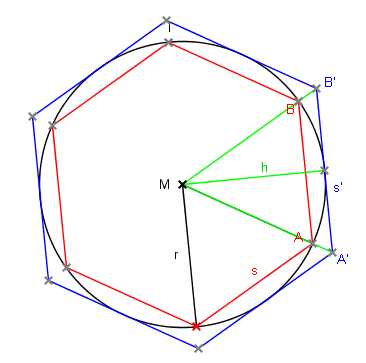
a) Gesucht: einbeschriebenes bzw. umbeschriebenes Sechseck mit Seitenlänge s bzw. s' (Lösung s. Figur)

b) Gesucht: Differenz der beiden Flächeninhalte F und F' der Sechsecke

Lösung:
Da s = r (Dreieck MAB gleichseitig), so ist F = 6 · 0.25 · √3 r² = 1.5 · √3 r²

Da auch Dreieck MA'B' gleichseitig und h = r, so ist h = 0.5 · √3 s' = r,
also s' = 2r/√3 , also (s' )² = 4 r²/3
Daher ist F' = 6 · 0.25 · √3 (s' )² = 2 · √3 r²

Damit folgt für die Differenz F' - F = 0.5 · √3 r²

c) Gesucht: Verhältnis der Umfänge u und u' der beiden Sechsecke

Lösung:
u' : u = s' : s = 2r/√3 : r = 2/√3