menu Logomathematik.ch

Geschichte der Mathematik: Zeittafeln Algebra, Geometrie, Analysis

Rhind-Papyrus

Hauptinformation über die ägyptische Mathematik: Rhind Papyrus (nach dem schottischen Ägyptologen Alexander Henry Rhind, der das Papyrus im Jahr 1858 kaufte). Es stammt vom Schreiber Ahmes (1680 - 1620 v.Chr.). Dieser wiederum gab an, dass die Informationen auf dem Papyrus bereits in den Jahren 2000 v.Chr. bekannt waren.

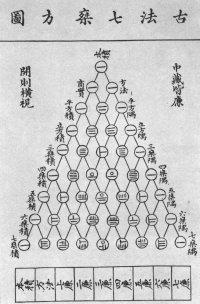
pascaldreieck

Altchinesische Mathematik um 1303
(das später nach Blaise Pascal benannte Dreieck)

Zeittafel Klassische Algebra
2. Jahrtausend vor Christus Die Ägypter lösen lineare Gleichungen mit einer Unbekannten
2. Jahrtausend vor Christus Die Babylonier lösen Systeme von zwei linearen Gleichungen mit zwei Unbekannten
2. Jahrtausend vor Christus Die Babylonier behandeln Gleichungssysteme, die auf quadratische Gleichungen führen
3. Jahrhundert nach Christus Die Griechen verwenden bei der Lösung von Gleichungssystemen Symbole für die Rechenoperationen
9. Jahrhundert nach Christus Al-Khwarizmi entwickelt Methoden zur Lösung quadratischer Gleichungen
1545 Cardano veröffentlicht Lösungsmethoden für die Gleichungen dritten Grades
1591 Vieta verwendet in der Theorie der Gleichungen Buchstaben statt Zahlen
1614 John Napier veröffentlicht die ersten Werte für Logarithmen
1620 Jost Bürgi veröffentlicht "Arithmetische und geometrische Progresstabuln" über natürliche Logarithmen
1637 Descartes stellt den Zusammenhang zwischen dem Grad einer Gleichung und der Zahl ihrer Lösungen fest
1799 Gauss beweist in seiner Dissertation den Fundamentalsatz der Algebra:
'Jede Gleichung n-ten Grades hat genau n komplexe Lösungen'
1824 Niels Abel beweist, dass es für Gleichungen ab 5. Grad keine allgemeine Lösungsformeln gibt
Ab 1824 Beginn der 'modernen' Algebra mit Evariste Galois

Zeittafel Geometrie
2. Jahrtausend vor Christus Den Babylonier ist der später nach Pythagoras benannte Satz über die Beziehungen der Seiten in einem rechtwinkligen Dreieck bekannt
2. Jahrtausend vor Christus Die Ägypter benützen eine Näherungsformel für die Berechnung der Kreisfläche
2. Jahrtausend vor Christus Die Ägypter berechnen das Volumen eines Pyramidenstumpfs
um 440 vor Christus Hippokrates v. Chios berechnet die Flächen von Möndchen
um 220 vor Christus Apollonios v. Perge definiert die Ellipse als Kegelschnitt
1636 Verbindung von Algebra mit Geometrie: Pierre de Fermat führt Koordinatensysteme ein
1637 René Descartes stellt eine Hyperbelgleichung auf
1822 Erfindung der projektiven Geometrie: Victor Poncelet untersucht projektive Eigenschaften
1900 David Hilbert führt die strenge Axiomatik in der Geometrie ein

Zeittafel Analysis
3. Jahrhundert vor Christus Archimedes berechnet eine unendliche Reihe
3. Jahrhundert vor Christus Archimedes berechnet den Inhalt eines Parabelsegmentes
1615 Infinitesimale Methoden: Kepler berechnet den Inhalt von Rotationskörpern
1629 Anfänge der Differentialrechnung: Fermat bestimmt Maxima und Minima
1635 Cavalieri berechnet den Flächeninhalt der allgemeinen Parabel
1670 Zusammenhang zwischen Diff.- und Integralrechnung: Barrow entdeckt den Hauptsatz der Differential- und Integralrechnung pdficon
um 1675 Erfindung des Calculus: Leibniz erfindet die moderne Differentialrechnung
um 1675 Anwendung auf Physik: Newton berechnet Bewegungsvorgänge
1755 Die ersten Lehrbücher: Euler differenziert die sinus-Funktion

Literatur: Popp, Walter: Wege des exakten Denkens, Ehrenwirth Verlag München 1981
amazon
4000 Jahre Algebra
4000 Jahre Algebra
H-W. Alten, A.D. Naini..		 5000 Jahre Geometrie
5000 Jahre Geometrie
H-W. Alten, A.D. Naini..		 Die Geschichte der Null
Die Geschichte der Null
R. Kaplan, E. Kaplan
Das unendliche Denken
Das unendliche Denken
Robert Kaplan		 Geschichte der Mathematik
Geschichte der Mathematik
H. Kaiser, W. Nöbauer		 ohne Bild
Wege des exakten Denkens
Walter Popp