Brachystochronen-Problem

Das Problem der Brachystochrone wurde 1696 von Johann Bernoulli öffentlich gestellt.
Wenn zwei Punkte P₁ und P₂ gegeben sind, die auf verschiedener Höhe (aber nicht untereinander) liegen, dann sollte unter allen möglichen Verbindungskurven, auf denen sich ein materieller Punkt unter dem Einfluss der Schwerkraft (ohne Berücksichtigung der Reibung) von P₁ nach P₂ bewegt, diejenige aufgefunden werden, für die die Zeit des Durchlaufens ein Minimum wird.

Folgende Information stammt aus dem Buch "Kleine Enzyklopädie - Mathematik", 1977, Verlag Harri Deutsch, Thun und Frankfurt/M.

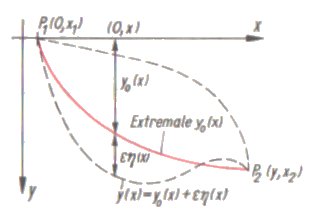
In einem passend gewählten Koordinaten­system sind zwischen den Punkten P₁ und P₂ einige solcher Verbindungskurven y = y(x) als mögliche Fallkurven eingezeichnet.
Da in jedem Punkt dieser Kurven der Weg s, die Zeit t und die momentane Geschwindigkeit v durch die Beziehungen \(\rm v=\large\frac {ds} {dt}\) verknüpft sind, da die durch die Erdbeschleunigung g erhaltene Geschwindigkeit den Wert \(\rm v=\sqrt {2gy}\) hat und das Bogenelement ds schliesslich die bekannte Funktion \(\rm ds=\sqrt {1+y'^2}dx\) von y’ und x ist, erhält man die zum Durchlaufen nötige Gesamtzeit T als ein bestimmtes Integral zwischen den Grenzen x₁ und x₂:
Aus \(\rm dt=\large\frac {ds} {\sqrt{2g y}} = (\frac {\sqrt {1+y'^2}} {\sqrt{2g y}})\normalsize dx \) folgt \(\rm T = \large\frac 1 {\sqrt{2g}} \Large\int_{x_1}^{x_2}\large{(\frac {\sqrt {1+y'^2}} {\sqrt{y}})\normalsize dx} \)

Dieses Integral soll für eine gesuchte Funktion y₀ = y₀(x) den kleinsten Wert haben, d.h., sein Wert ist für alle von y₀ verschiedenen Funktionen y*(x) grösser. Dies ist ein Variationsproblem ohne Nebenbedingungen. Euler gelang es, das Variationsproblem auf Differentialgleichungen zurückzuführen. Er ging davon aus, dass alle zur Konkurrenz zugelassenen Funktionen y(x) sich in den Punkten P₁ und P₂ nicht von der gesuchten Extremalen y₀(x) unterscheiden dürfen. Er dachte sich y(x) stets zusammengesetzt aus der Extremalen y₀(x) und einer Abänderungsfunktion εη(x).
Nach der Lösung der dazugehörigen Eulerschen Differentialgleichung erhält man mit α als Parameter und zwei Konstanten C₁ und C₂ als Lösung die Zykloide
x₀ = ±\(\bold {\large\frac {C_1} {2}}\)(α - sin α) + C₂
y₀ = \(\bold {\large\frac {C_1} {2}}\)(1 - cos α)