Peripherie- und Zentriwinkel

Es gilt der Satz:

Ein Zentriwinkel ist doppelt so gross wie ein Peripheriewinkel über dem gleichen Bogen
(gilt auch für stumpfe Peripheriewinkel)

Folgerung:

Alle Peripheriewinkel über dem gleichen Bogen sind gleich gross

Prüfen Sie diese Behauptungen an folgender Figur:
Sie können den Scheitel P des Peripheriewinkels mit der Maus (auf dem Kreis) bewegen. Alternativ können Sie auch mit 'Step' die Lage von P schrittweise verändern.
Durch Verschieben der Ecke B (Radiobutton aktivieren) verändern Sie den Zentriwinkel und damit auch den dazugehörigen Peripheriewinkel.
Immer gilt aber: Zentriwinkel = 2*Peripheriewinkel
Sie können dadurch auch den Satz des Thales experimentell nachvollziehen:
Der Peripheriewinkel über dem Kreisdurchmesser AB (also Zentriwinkel = 180°) misst 90° → Thaleskreis.

Zentriwinkel = °

Peripheriewinkel = °

Lage Punkt P verändern

Lage Punkt B verändern

Thaleskreis

Anwendung dazu: Ortsbogen 70°, Lösung 1

Beweis für spitzen Peripheriewinkel:

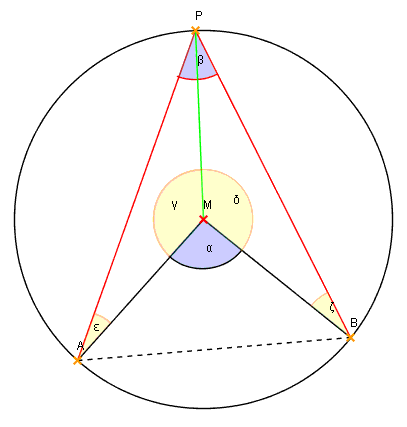
Zentriwinkel α, Peripheriewinkel β
Behauptung: α = 2β

Da Dreieck APM gleichschenklig, so
∠(APM) = ∠(PAM) = ε. Also ist γ = 180° - 2ε

Da Dreieck APM gleichschenklig, so ∠(BPM) = ∠(PBM) = ζ. Also ist δ = 180° - 2ζ

Also ist α = 360° - γ - δ = 2ε + 2ζ

Da aber β = ε + ζ, so gilt die Behauptung
(für stumpfen Peripheriewinkel β analog)